In this series we'll look at generic PDP-11 code which will work on any system with a PDP-11 CPU!

Lesson M1 - Random Numbers and Ranges Lets look at some tasks we'll need to make a game... we'll look at generating random numbers, and checking if they fit within a certain range.

SuckRT.mac Rand.mac

The Random number generator shown today is far from the 'Best'... but it does work! It's used in these tutorials by all the games as it's been tested without any problems, and has been ported to many different systems and CPUs, and given the same random seed, it gives the same results... meaning it can be used for generating random levels in your game, and the level will be the same on every system.

To allow our random number generator to create good varied results, we use a pair of 16 byte lookup tables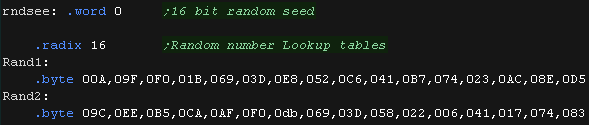
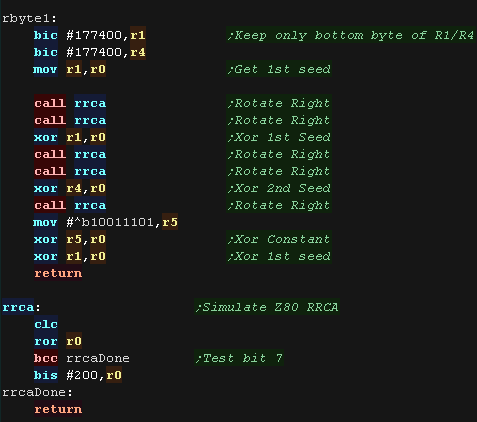
Our random number generator produces a 16 bit result (one byte in R3 and R5) from a 16 bit random seed (r1). The 'High byte' of the 16 bit pair is created by bitshifting and combining the two.
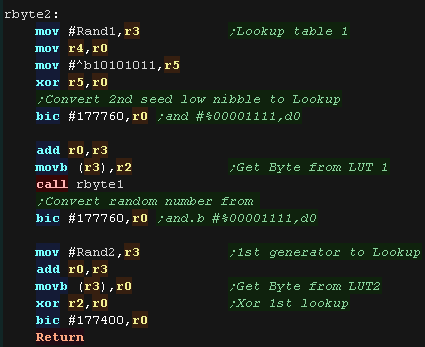
We need the 'Low byte' to be very different, or the 16 bit values won't be very random! We use the lookup tables to get some new data, and combine these to produce the second value
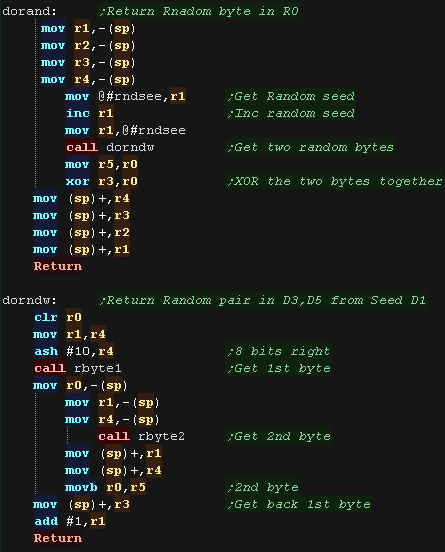
We have two routines we can use to get values "DoRandomWord" will get a 16 bit value zHL from seed zBC, this can be used to produce 'psuedorandom' data for times we want repeatable results. "DoRandom" is an easy function to return an 8 bit byte in the Accumulator... it automatically updates its seed every time.

To be usable, a random number generator needs to produce every possible random number (0-255 or 0-65535)... otherwise you could have serious problems with your program (if you're waiting for a result that never happens). The more 'random' the data the better... that is, if you plotted the values on a graph there should be no patterns present.

Range checking

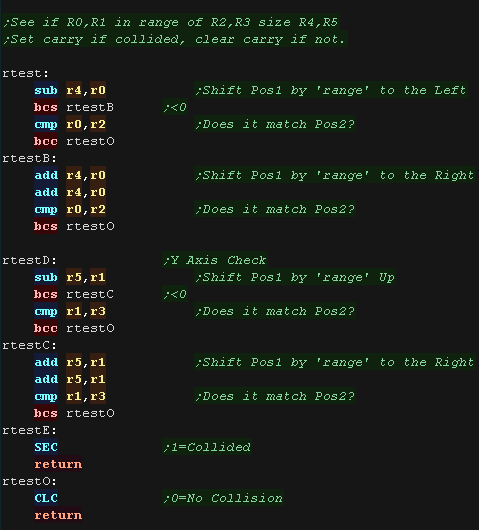
We need to do 'Collision detection'. We specify a two targets and a 'range' ... if target 1 is within 'Range' of target 2, we return with the Carry set... if it's out of range we return with the Carry clear... This means we can do a BNE or BEQ on return.

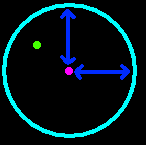The range check is simple... we test X and Y axis We test the X axis first. we subtract the 'RANGE' from each axis of the object, and check if we went below Zero (if so that direction is over the limit)... we then compare to the position... if it's lower we're out of range... if not we need to test more! Next we add 'RANGE' twice... once to move back to the center and once to move to the right... we then compare to the position... If it's higher we're out of range... if not we need to test the Y axis! We repeat the same tests for the Y axis.

Lesson M2 - Binary coded decimal In games we may wish to use binary coded decimal to store scores in a way that's easy to convert to Ascii Here we'll look at some simple routines to support BCD on PDP11.

BCD_Test.asm

The Battle for BCD

Converting large numbers from Hex to Ascii is hard! A common simple solution to this is Binary Coded Decimal... This stores a single 0-9 digit in each nibble -  Two per byte, This is known as PACKED BCD! This is easier to show to screen than normal hex numbers.
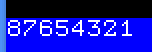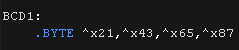BCD only uses a 0-9 value in each nibble... but of course each nibble can really support 0-F Suppose we repeatedly add 1 to the value 8... we'll need to correct the value once the value goes over 9 values like $0A will need to be converted to the correct BCD value of $10... and we'll need to do that ourselves!	$08 +1 $09 +1 $0A -> $10
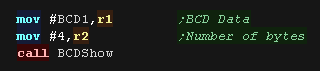
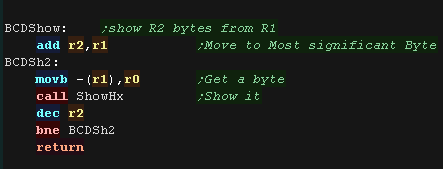
To ShowBCD, we need to step through each of the 8 digits in our 32 bit value..... here we'll show R1 to the screen we rotate a digit (nibble) out of R1 into R0, add #48 to convert it to Ascii, and show it to the screen with PrintChar We repeat until all 8 characters are shown.
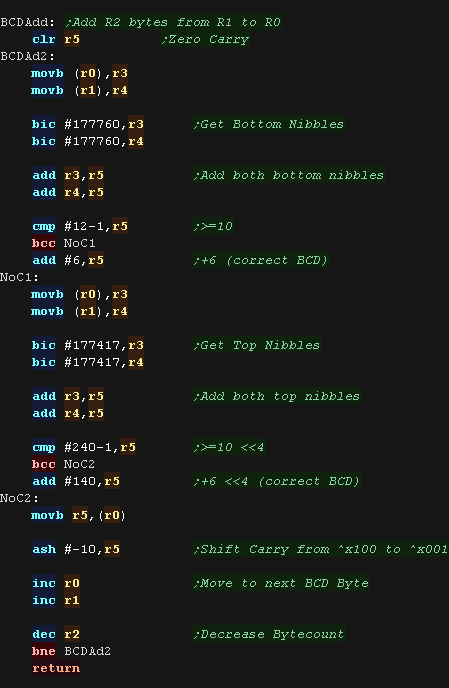
We'll need to AddBCD to add score... but this is a little more tricky! Here we're adding our values one digit at a time, but we need to cope with any carry!... We split each byte into 2 nibbles, and process each nibble separately If a digit goes over 9, we need to add 6, skipping over the A-F part of the nibble, and storing any carry for the next digit in R5 we repeat for all 8 digits.
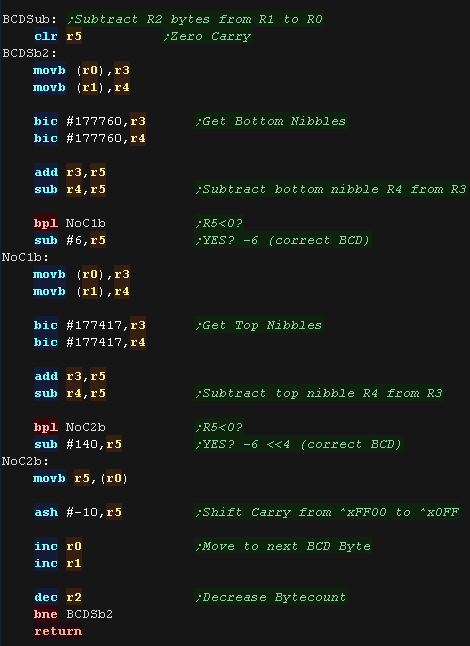
We can write SubBCD to subtract BCD in a similar way Once again we work through the digits keeping track of the carry.
If we want to compare two BCD sequences, this is pretty easy! We just need to step through the sequence from the most signigicant byte until we find a byte which is not equal in both BCD values We then return with the flags set according to the result of that comparison. If we find no difference, the two sequences are the same.