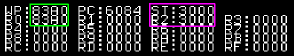Learn Multi platform TMS9900 Assembly
Programming... With Workspaces!

|
Don't like to read? you can learn while you
watch and listen instead!
Every Lesson in this series has a matching YOUTUBE video... with
commentary and practical examples
Visit the authors Youtube
channel, or Click the icons to the right when you see them
to watch the Lessons video! |
 |
The TMS9900 is a 16 bit CPU, a miniature version of the TI 990
minicomputer, it was designed for home computer use, but it was
really only used in the Ti-99
Despite it's failure in the market the TMS9900 is a fascinating
chip, it has virtually no registers, instead using 'Workspaces'...
banks of 32 bytes that make the 16 registers (like a zeropage)...
it also has no stack! |

|
When a function is called, one register is used as a 'Link pointer' -
pointing to the return address... if we need new registers for our
subroutine, we allocate another 'workspace' giving us a new set of
registers - when we're done we restore the original workspace.
 |
If
you
want to learn TMS9900 get the Cheatsheet!
it has all the TMS9900 commands, it also covers the extra
commands used by the 65c02 and PC-Engine HuC6280
|
 |
Systems covered in these tutorials
ChibiAkumas Tutorials
Useful Documents
What
is the TMS9900 and what are 8 'bits' You can skip this if
you know about binary and Hex (This is a copy of the same section in the
Z80 tutorial)
The TMS9900 is an 16-Bit processor with a 15 bit Address bus (meaning data
operations must be word aligned)
What's 8 bit... well, one 'Bit' can be 1 or 0
four bits make a Nibble (0-15)
two nibbles (8 bits) make a byte (0-255)
two bytes (16 bits) make a word (0-65535)
And what is 65535? well that's 64 kilobytes
... in computers 'Kilo' is 1024, because binary works in powers of 2, and
2^10 is 1024
64 kilobytes is the amount of memory a basic 8-bit system can access
Numbers in Assembly can be represented in different ways.
A 'Nibble' (half a byte) can be represented as Binary (0000-1111) ,
Decimal (0-15) or Hexadecimal (0-F)... unfortunately, you'll need to
learn all three for programming!
Also a letter can be a number... Capital 'A' is stored in the
computer as number 65!
Think of Hexadecimal as being the number system invented by someone wit h
15 fingers, ABCDEF are just numbers above 9!
Decimal is just the same, it only has 1 and 0.
|
NASM /ASW
TMS9900 assembler
|
classic
TI99 Assembler
|
Decimal
|
123 |
123 |
Hex
|
0FF00h |
>FF00 |
Binary
|
00110011b |
|
Ascii
|
"A" |
'A' |
ASW and Byte definitions
Be careful with BYTE definitions - they are
automatically Word aligned... EG
BYTE 1
BYTE 2
Will produce data 1,0,2,0 ... You probably
want
BYTE 1,2
instead which will result in 1,2
We're going to use
Macro AS in these tutorials, it uses the same syntax as Intel
x80 chips... this is very different to the original TI99
Assemblers, but will make it easier for us to learn.
|
 |
| Decimal |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
... |
255 |
| Binary |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
|
11111111 |
| Hexadecimal |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
FF |
Another way to think of binary is think what each digit is 'Worth'
... each digit in a number has it's own value... lets take a look at
%11001100 in detail and add up it's total
| Bit position |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
| Digit Value (D) |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
| Our number (N) |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
| D x N |
128 |
64 |
0 |
0 |
8 |
4 |
0 |
0 |
| 128+64+8+4= 204
So %11001100 = 204
! |
If a binary number is small, it may be shown as %11 ... this is the
same as %00000011
Also notice in the chart above, each bit has a number, the bit on
the far right is no 0, and the far left is 7... don't worry about it
now, but you will need it one day!
If you ever get confused, look at Windows
Calculator, Switch to 'Programmer Mode' and it has binary
and Hexadecimal view, so you can change numbers from one form to
another!
If you're an Excel fan, Look up the functions DEC2BIN and DEC2HEX...
Excel
has all the commands to you need to convert one thing to the
other! |
 |
But wait! I said a Byte could go from 0-255 before, well what
happens if you add 1 to 255? Well it overflows, and goes back to 0!...
The same happens if we add 2 to 254... if we add 2 to 255, we will
end up with 1
this is actually usefull, as if we want to subtract a number, we
can use this to work out what number to add to get the effect we want
| Negative number |
-1 |
-2 |
-3 |
-5 |
-10 |
-20 |
-50 |
-254 |
-255 |
| Equivalent Byte value |
255 |
254 |
253 |
251 |
246 |
236 |
206 |
2 |
1 |
| Equivalent Hex Byte Value |
FF |
FE |
FD |
FB |
F6 |
EC |
CE |
2 |
1 |
 |
All these number types can be confusing,
but don't worry! Your Assembler will do the work for you!
You can type %11111111 , &FF , 255 or -1
... but the assembler knows these are all the same thing!
Type whatever you prefer in your ode and the assembler will work
out what that means and put the right data in the compiled code! |
The TMS9900 is a BIG
ENDIAN machine... what's stranger is that byte operations (like
MOVB) work with the TOP BYTE of the register.
Words must be loaded from EVEN addresses, if
an attempt is made to load from an ODD address, the bottom bit 0 will be
ignored (causing a word read from 1001 to read in from 1000)
The 3 real registers in the CPU are
as follows
| Register |
Purpose |
| PC |
Program Counter |
| WP |
Workspace Pointer |
| ST |
Status |
The 16 Workspace registers (in ram) have the following Names and
functions
| Register |
Purpose |
| R0 |
Bits 12-15 Shift Count
Cannot be used as an Index register with @Table(R) |
| R1 |
- |
| R2 |
- |
| R3 |
- |
| R4 |
- |
| R5 |
- |
| R6 |
- |
| R7 |
- |
| R8 |
- |
| R9 |
- |
| R10 |
- |
| R11 |
Return address (PC � BL) |
| R12 |
CRU Addressing |
| R13 |
Context Switching (WP � BLWP) |
| R14 |
Context Switching (PC � BLWP) |
| R15 |
Context Switching (ST � BLWP) |
|
|
Flags:
L>
A> EQ C OV OP X -
/ - - - - I I I I
Flag
|
Meaning
|
Bit Details
|
| L> |
Logical Greater than |
|
| A> |
Arithmetic Greater than |
|
| = |
Equal |
|
| C |
Carry |
|
| O |
Overflow |
1=overflow?
|
| P |
Parity |
|
| X |
Xop |
|
| I |
Interrupt Mask |
|
|
The TMS9900 Addressing Modes
The TMS9900 has 8 different addressing modes... many are similar to much
later systems... in addition it has 4 'effective modes' which are defined
by using Reg 7 as a parameter
'Deferred' addressing is known as indirect
addressing on other systems
| Syntax |
Effect |
| R |
Workspace Regsiter Addressing |
| *R |
Workspace Register Indirect Addressing |
| *R+ |
Workspace Register Indirect Auto Increment Addressing |
| @Label |
Symbolic (Direct) Addressing (R=0) |
@Table(R)
|
Symbolic Indexed Addressing (doesn't work with R0) |
| n |
Immediate Addressing |
?
|
Program Counter Relative Addressing |
?
|
CRU Relative Addressing (R12) |

Structure of an ASM (.MAC) source
file
Lets look at a simple file (Minimal.asm)
we have a header - We're including a
header to do our setup, and calling the screen initialization
routine. (BL = Branch and Link)
In our body we're running a simple
monitor program - this is where you would put your code
In our footer we're including some useful
files (with include statements)
This example will show a hello world message, the status of the
registers, and dump some bytes of memory. |
 |
 |
The Include
files are doing most of the work for us here - this will give
you an easy starting point to begin learning, but you'll want
to modify it and make something of your own once you're more
experienced
|
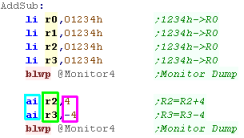
Loading Values
Lets load a value into a register...
We're going to Load an Immediate value into a register with LI
The Destination register is on the Left
(R0)
The source value is on the Right (1234 in
decimal)
Immediate values must be fixed numbers... LI R0,R1 will not work! |
 |
By default a number will be treated as Decimal.
We can specify Hex by putting a h at the end...
we'll need to make sure it starts with a number, so if the first
digit is A-F add a 0
We can specify Binary by putting a b at the end
We can specify Octal by putting an o at the end
|
 |
Here are the results
|
 |
| We can use Ascii if we put our characters in apostraphe '--'...
each register can hold 2 characters |
 |
| Here is the result |
 |
Moving values between registers
| If we want to transfer data
between registers we use MOV ... the source
is on the left, the destination is on
the right |
 |
Lets try a variety of move commands
We'll copy R0 into R1,R2 and R3 |
 |
| Here is the result |
 |
One word (16 bit) commands to set values
There are two special
commands that don't need a parameter (making them faster)
We can set a register to zero with CLR
We can set a register to all 1 bits (FFFFh) with SETO
(SET Ones) |
 |
| Here is the result |
 |
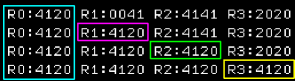
Addition and Subtraction
When we want to Add or Subtract a fixed Immediate value we use AI (Add Immediate)...
The destination register is on the left of
the comma, the amount to add is on the
right,
There is no subtract version, but the amount to add can be
negative! |
 |
| Here is the result |
 |
If we want to add a register to
another we use A (add)... the source is on the
left, the destination is on the right.
If we want to subtract a register from
another we use S (add)... the source is on the
left, the destination is on the right. |
 |
Here is the result
|

|
Adding or Subtracting by 1 or 2
quickly
There will be many times when we want to increase or decrease by
1 or 2 (for loops or addresses)... we have single commands to do
this!
INC will INCrement a register by 1
DEC will DECrement a register by 1
INCT will INCrement a register by 2
DECT will DECrement a register by 2
We'll do this four times. |
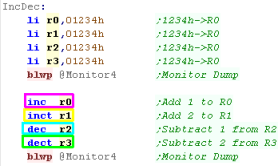 |
| Here is the result |
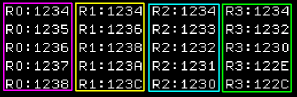 |
Don't forget, you can only load Words from even
addresses!
If you try to load from an odd address like 1001h it will actually
read from address 1000h... so don't do it!
Code will mess up too... so make sure if data segments exist in
your code they use even byte numbers... You can use Align 2 to
align data to an even boundary. |
 |
Lesson
2 - Addressing Modes on the TMS-9900
Lets take a look at the Addressing modes of the TMS-9900, In
this lesson we'll be looking at each addressing mode, and trying
out each with an example. |
 |
 |
|
 |
Immediate Addressing
Immediate addressing is where a fixed
numeric value is included in the line of code.
We can use a Symbol to define a text label
as EQUal to a number |

 |
| Here is the result. |
 |
Workspace Register Addressing
Workspace Registers are normal registers (R0-R15)
Workspace Register Addressing is the use of a register as the
source or destination of an operation... in the case of MOVe, the
source is on the Left, and the destination is on the right. |
 |
| Here is the result |
 |
Workspace Register Indirect
Addressing
We'll often want to load data from an address... and this
address may be in a register.
Workspace Register Indirect Addressing is where the source or
destination of an operation isn't a register... but the address in
the register.
This is denoted by an asterisk * before the
register - the address in the register will be used as the
source or destination |

 |
The registers will be loaded from the address in the register.
For example R3 has loaded 1122h from
the address 8300h in R0 |
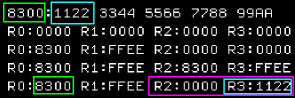 |
Workspace Register Indirect Auto
Increment Addressing
We've learned we can read from an address in a register by
prefixing with * , but many times we'll want that address to
change
For example, if we're reading sprite data, or filling an area of
ram with data.
We can automatically use the address in a register and increment
it by keeping the * prefix and adding a + |
 |
| Here are the results |
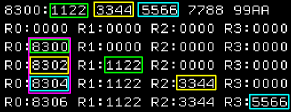 |
In this example
we've loaded two bytes, so the register went up by 2
If we use MOVB *R0+,R1 - then it will go up by 1.
|
 |
Symbolic (Direct) Addressing
This is where we are loading from a fixed
address... we just put an @ at the start of a number.
(without the @ it would be an immediate value)
We can also use a symbol if we wish
Remember... Words must be loaded on even boundaries... odd
boundary reads will malfunction |
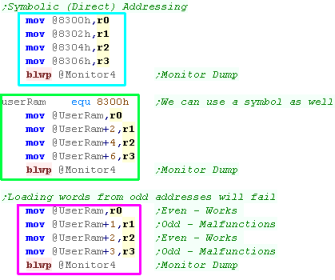 |
| Here are the results |
 |
Indexed Addressing
Indexed addressing uses the value in a register plus an offset
(index)... First we put an @ symbol, next the offset number, and a
register to use in brackets...
for example, look at the sample to the right ->
in this case the offset is 4 and the register is r3... if R3=10 then the final
address is 14 |
@4(R3) |
We can specify an index (offset) as a Positive
number or a Negative number
We can use Symbols to make things easier to
read.
Symbols will often be used to read offsets in data arrays...
For example a game object may have 8 bytes of data... an Xpos at
offset 0, Ypos at offset 2, Sprite Address at offset 4, and Speed
at offset 6
We would point our register to an object, and run the routines for
that object, then move the register to the next object and repeat
*** This command cannot use register R0 as the source *** |
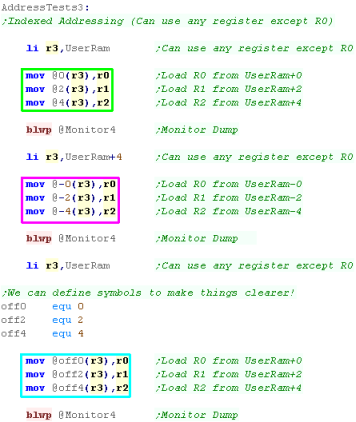 |
| Here are the results |
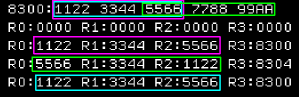 |
In most cases
these addressing modes can be used as the source or destination
of a command
If you try and addressing mode that isn't possible, the
assembler will soon tell you.. so give it a go!
|
 |
Lesson
3 - Comparisons and Byte commands
We've looked at basic commands for registers, and various
addressing modes, but we've just got started.
Although the registers are 16 bit, the TMS9900 has 8 bit 'byte
commands'... we also need to learn about compare commands...
lets learn about it! |
 |
 |
|
 |
Byte Commands
Byte commands on the TMS9900 are a bit weird... most processors
use the bottom byte of a register, but the TMS9900 uses the TOP
byte of the 16 bit registers!
To load an 8 bit byte, we use MovB (B for
byte)... this will load in from an address, or another register.
|
 |
Here is the result... note the difference between Word
and Byte commands...
The top byte is loaded in... the bottom byte is unchanged |
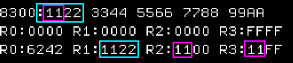 |
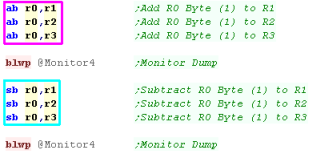
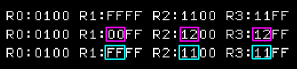
We can Add bytes with the AB command
We can Subtract bytes with the SB command |
 |
| Only the top bit is affected. |
 |
| We can swap the high and low byte of a register with SWPB |
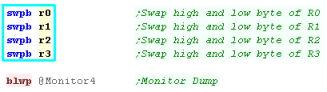 |
| Here is the result... top and bottom bytes of each register were
swapped. |
 |
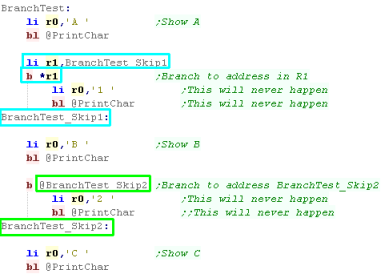
Branch (B)... Branch and Link (BL)
and Jump!
Branch would be called JMP (jump) on most processors... it
allows to move to a different address in the code without return
We can load an address into a register and branch to it with *
Alternatively we can specify a label (or
address) with the @ symbol, and the code execution will
continue from that point.
|
 |
if we want to call a subroutine and return we want to use BL
(Branch and Link)... we specify BL with @ and a
label
Because the TMS9900 doesn't have a stack, we need to handle the
return address... BL puts the return address in R11, and we can
return with B *R11
If we want to use R11 for something else (or a nested BL)
we'll have to do something else with it... for
example move it to R10 |
 |
| Here is the result. |
 |
 |
On systems like the 68000 BRAnch can only
jump short distances, but JuMP can jump anywhere.
On the TMS9900 it's the opposite!...JMP is for close
ranges...Branch can go anywhere!
|
Because we don't have a stack, nested subroutines
will have problems with re-using variables... and keeping the
return address is a pain.
However, there's a solution!
'Workspaces' give us a full set of new registers for our sub
(using 32 bytes of ram)... we'll learn about them soon! |
 |
Compare... Equals / Not Equals
(Zero / NZ)
Like most CPU's, we can use the status flags to do conditional
jumps (branches)
When we want to compare values, we have 3 options...
CI will compare a register to an immediate
C will compare 16 bit values in registers
CB will compare bytes (the top byte) of the
registers |
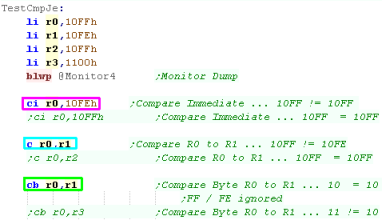 |
These commands will set the flags... when we want to actually
act on the comparison we need to use special Jump commands
JEQ will Jump if EQuals (if the zero flags
is set - if the difference is zero)
JNE will Jump if Not Equals (if the zero flag
is not set - if the difference is not zero) |
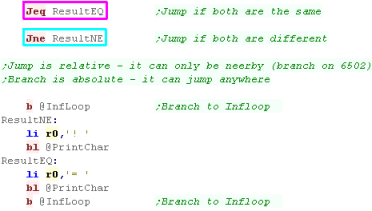 |
 |
The results
of these test will depend on the commands you run!
It's impossible to show enough screenshots to make it clear how
these commands work.
You'll need to download the examples, rem out and unrem some of
the lines, and see how the results change!... Quit being lazy!
go download the devtools!
|
Unsigned... Higher / Lower / Higher
or Equals / Lower or Equals
If we're working with Unsigned numbers, after a compare
we have four branch options.
JH will Jump if the first parameter is Higher
than the second
JL will Jump if the first parameter is
Lower than the second
JHE will Jump if the first parameter is
Higher or Equal to the second
JLE will Jump if the first parameter is
Lower or Equal to the second |
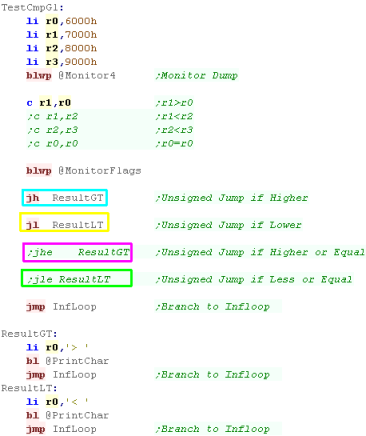 |
Signed... Greater Than / Less Than
If we're working with Signed numbers, we have two options
JGT will Jump if the first parameter is
Greater Than the second
JLT will Jump if the first parameter is
Lower Than the second
Note, that 7000h is a positive number... but 8000h is a negative
one (in signed numbers) so we must use the correct conditional
jump or we may get the wrong result! |
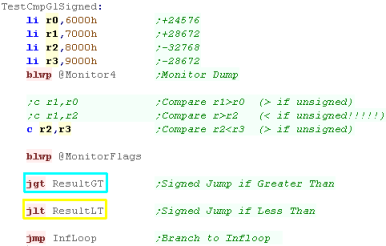 |
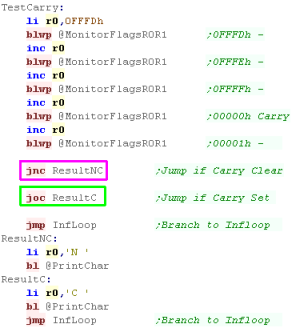
Carry Flag
The carry flag is set whenever an operation pushes a bit out of
a register - it's effectively the '17th bit' of a register
In this example, we'll repeatedly INC R0 until it overflows
(Setting the carry)...
We have two jump options
JNC will jump if there is No Carry
JOC will jump On Carry |
 |
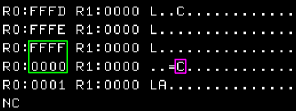
| When R0 rolls over... the Carry
Flag will be set. |
 |
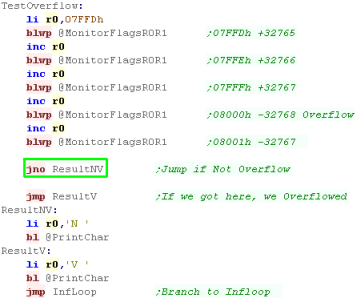
Overflow Flag
The Overflow flag is used
for Signed numbers...
The limit of a Signed number is -32768 to +32767 ... this causes a
problem!
If we have a register with 7FFFh in it (+32767) and we add
one it will change to 8000h... -32768!... the sign has flipped and
the number is invalid!
To detect this we have the overflow flag... we have only one Jump
option
JNO will Jump if there is No Overflow.
Of course, if execution continues without a jump that must mean
there was an overflow. |
 |
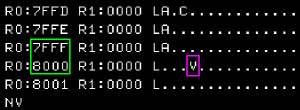
| When the register overflows the oVerflow
flag will be set |
 |
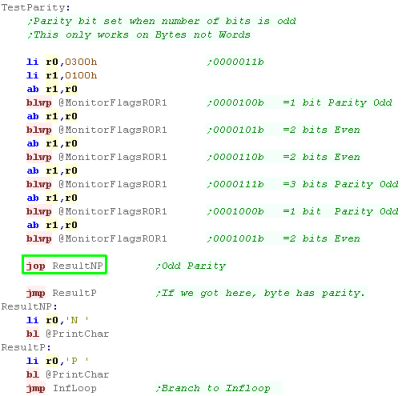
Parity Flag
Parity is a bit special!...
it's designed for error checking - for example, when reading data
from tape or punched cards
It only works on byte commands.
The parity flag is set according to whether the count of '1' bits
in the byte is odd or even
To detect this we have the Parity flag... we have only one Jump
option
JOP will Jump on Odd Parity
Of course, if execution continues without a jump that must mean
parity was even. |
 |
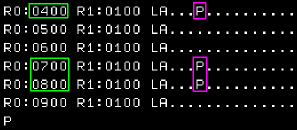
| When the '1 bit count' is odd... the
Parity flag is set |
 |
Lesson
4 - Wonderous workspaces and Mega Maths!
It's time to learn how the TMS9900 copes without the stack
(Spoiler: Workspaces!)
We'll also learn about the Multiplication and Division commands. |
 |
 |
|
 |
What's these workspaces?
All
through these tutorials we've used Registers R0-R15 for various
purposes...
However these are not 'Registers' like BC and DE are on the Z80,
or X and Y are on the 6502... These are actually held in an area
of memory called the 'Workspace'...
Effectively they are like the Zero page on the 6502
In fact the TMS9900 only has 3 'true' registers in the CPU...
WP,PC and ST - they're all 16 bit.
WP is the Workspace Pointer - this points to the start of a 32
byte (0020h) range of memory used by workspace registers R0-R15
(the ones we've used so far!)
PC is the program counter - this is the pointer to the running
byte of our program
ST is the STatus flag register |
Before we can use the WorkSpace Registers we need to define the
Workspace Pointer
We do this with LWPI ... Load Workspace
Pointer from Immediate
The Header (V1_Header.asm) has been doing this for us in these
tutorials... it's been setting the workspace to Ram address 83C0h
(Ram is from 8300-83FFh) |
 |
BLWP - Branching and Linking with a new Workspace Pointer
Before we used Branch and Link - but we had to be careful with
R11 (the return address) making nesting difficult or impossible -
we also had to ensure we didn't change any other registers which
could cause problems.
The solution is BLWP - this will keep the old registers intact,
and use a different 32 bytes of memory for a new set of Workspace
registers - when we return, the old workspace will be restored,
keeping the old registers intact!
We do this with BLWP - this points to a
Transfer VECTOR - Two Words which will define the the new vector. |
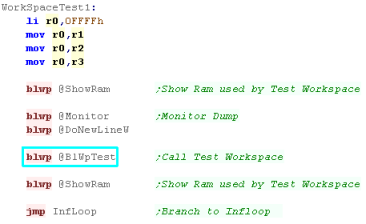 |
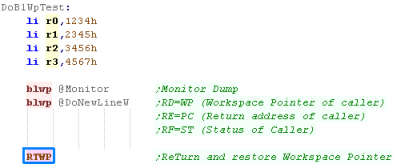
BLWPTEST is the Vector table - it contains two words
The first is the address in RAM for the new
workspace for registers R0-R15 (32 bytes)... this goes into
register WP
The Second is the address of the subroutine
where execution will resume... this goes into register PC
|
 |
When BLWP occurs some of the previous register values are
transferred.
Old Register (Before BLWP)
|
New Register (after BLWP) |
| WP (Workspace Pointer) |
R13 |
| PC (Program Counter) |
R14 |
| ST (STatus Flags) |
R15 |
| Transfer Vector Word 1 |
WP (Workspace Pointer) |
| Transfer Vector Word 2 |
ST (STatus Flags) |
R13,R14 and R15 are used by the return command RTWP
(ReTurn Workspace Pointer) - so must not be changed by the
subroutine.
RTWP will restore the original Workspace, and carry on with the
command after BLWP
Our Test Sub just makes a few registers changes as an example then
returns |
|
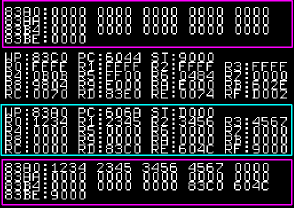
The Subroutine used 83A0h as it's workspace...
The Register changes of this subroutine can
be seen in ram after it runs. |
 |
We can nest
subroutines using BLWP again within our subroutine just fine...
PROVIDING the subroutine does not use the same Workspace Ram as
one of it's parents
Otherwise the return address would be corrupted ... Also Two
different Subs can have the same WorkSpace providing they won't
be nested within each other
You can always have different Transfer Vector Tables - with
different choices of workspace depending on the nesting!
|
 |
 |
In theory, you could never use BL, and just
use BLWP... but remember the TI99/4A only has 256 bytes of
RAM... Enough for just 8 workspaces... so you'll need to try to
limit yourself to as few workspaces as possible.
|
Working with WP (Workspace Pointer)
and ST (STatus flags)
Apart from BLWP and RTWP there are 3 special commands for
working with WP and ST registers
LWPI is Load Workspace Pointer from Immediate
- this is how we set our default workspace pointer
STWP is STore Workspace Pointer - this
transfers the current Workspace Pointer to a register (R0-R15)
STST is STore STatus register - this
transfers the current STatus flags to a register (R0-R15) |
 |
WP was transferred to R0
ST was transferred to R2 |
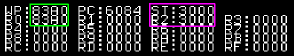 |
Multiplication and Division... in 32 bit!
Regular commands are all 16 bit... but MPY and DIV are different
When it comes to Multiplication and Division a pair of registers
are combined into a High.Low pair.... we specify the first, and
the following register will be used as well so if we specify R0
then R0+R1 would be used as a pair.
mpy r0,r2 will Multiply R0 by R2... the
result will be stored in R2.R3 (R2 = High Word / R3 = Low Word)
div r0,r2 will Divide R2.R3 by R0 ... the
'whole number' result will be stored in R2... any remainder will
be stored in R3
|
 |
In this example we first Multiplied R0 by
R2... The result was stored in R2.R3
|

|
| Next We Divided R2.R3 by R0...
The result was stored in R2 - the
remainder was in R3 |

|
| Where as most commands can use any addressing mode
as a source or destination, the 32 bit register pairs will not
work with memory addresses. |
 |

Lesson
5 - Bit Operations.
We're nearly at the end of our tutorials... but we've not
yet looked at the Bit shift and Logical Operations'
We'll also have a look at a few other 'conversion commands' for
switching values around |
 |
 |
|
 |
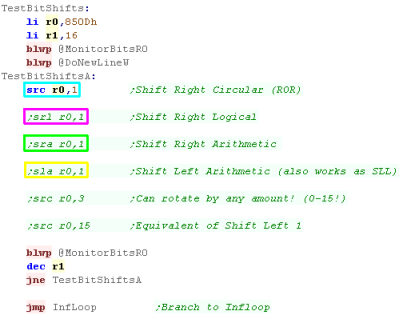
Bit Shifts
The TMS9900 has a variety of bit shifting commands... what's
better is they all allow a shift amount of 0-15!
The commands available are:
SRC - Shift Right Circular (ROR on the 68000)
SRL - Shift Right Logical
SRA - Shift Right Arithmetic
SLA - Shift Left Arithmetic (Also works as
SLL)
All these work with shift sizes of 0-15...SRC with a shift of 15
would effectively act like Shift Left Circular (SLC doesn't
actually exist) |
 |
| SRC will shift the bits to the right, bits
that drop off the right side will reappear on the left |
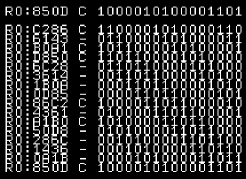 |
SRL will shift the bits to the right,
New bits that appear on the left will be zero
This will halve an unsigned number, but may break a signed one |
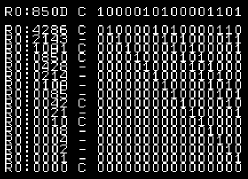 |
SRA will shift bits to the right - New
bits that appear on the left will be the same as the last top bit
This will halve an signed number, but may break an unsigned one |
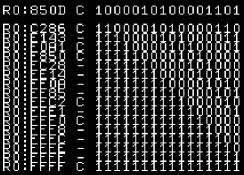 |
SLA will shift bits
to the left - New bits that appear on the right will be zero
This will halve an signed or unsigned number. |
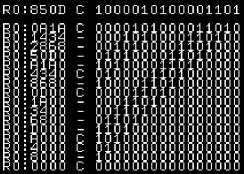 |
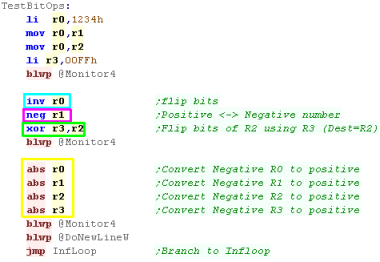
Bit based Mathematical transformations
There are a few mathematical
operations that alter register values relating to bits (?)
NEG r1 converts a positive to negative and
vice versa - effectively flipping all the bits and adding 1
INV r1 will flip all the bits in a
register.
XOR r1,r2 will flip the bits of r2 where a
bit in R1 is 1... effectively if r1=FFFFh then this is the same as
NEG
ABS will remove the negative sign from a
negative number... it will have no effect on a positive number |
 |
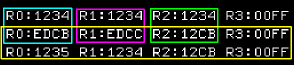
Here are the results of the commands.
|
|
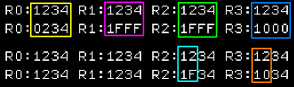
Logical Ops, Set and Clear
We have 6 logical operation commands... though two
are just 'byte versions' of others.
ANDI will AND an immediate value -
effectively zeroing bits in R0 which are not 1 in the parameter
ORI will OR an immediate value -
effectively setting to 1 bits in R0 which are 1 in the parameter
SOC Sets to 1 any bits in the destination
that are 1 in the source... it's effectively the same as OR
SZC sets to 0 any bits in the destination
that are 1 in the source... it's the equivalent of AND where all
the bits of the parameter are flipped.
SOCB is the same as SOC, but works on the top
byte of the register (BYTE)
SZCB is the same as SZC, but works
on the top byte of the register (BYTE) |
 |
| Here is the result |
 |
Compare ones, compare Zeros
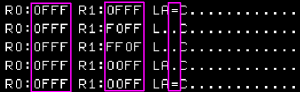
We have some special commands for comparisons
COC will 'Compare ones corresponding'...
this will check all the 1's in the first parameter, are 1 in the
second... setting the zero flag accordingly |
 |
| The zero flag changes according to the
values in the two parameters. |
 |
| CZC will 'Compare Zeros
corresponding'....this will check all the 1's in the first
parameter, are 0 in the second... setting the zero flag |
 |
| The zero flag changes according to the
values in the two parameters. |
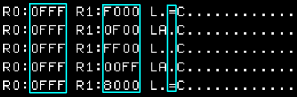 |
COC and CZC
are the closest we have to BIT or BTST commands on the TMS9900,
They're a bit weird compared to the Z80, but the PDP-11 was also
similar in it's commands.
|
 |